Función seno

En un ángulo interno en el círculo trigonométrico cuyos segmentos son igual al radio 1, el seno será la proyección del segmento móvil sobre el eje de las ordenadas Y. Imaginemos una linterna iluminando este segmento móvil dentro del círculo. La sombra que proyecta el segmento sobre el eje Y será el valor del seno.
Cuando se grafica el seno a medida que el segmento se abre, el seno crece hasta ser igual a 1, cuando el ángulo es igual a 90º o 1/2π. Desde los 90º a los 180º el seno se reduce pero sigue siendo positivo. Por encima de los 180º el seno toma valores negativos hasta llegar a los 360º. Los valores del seno se hallan entre 1 y -1.
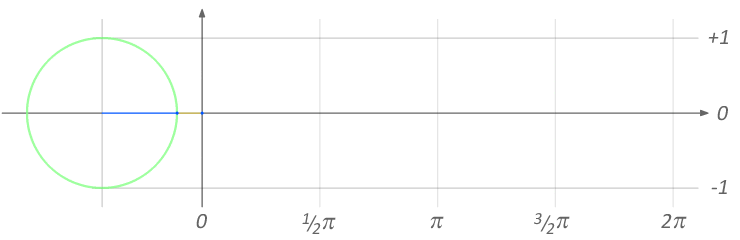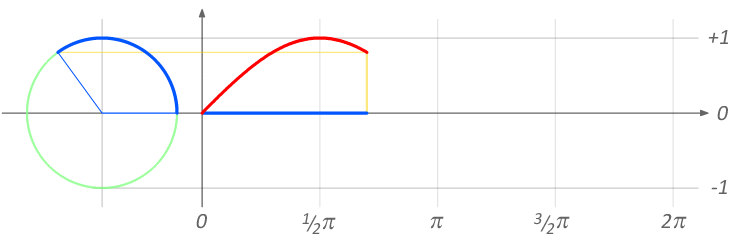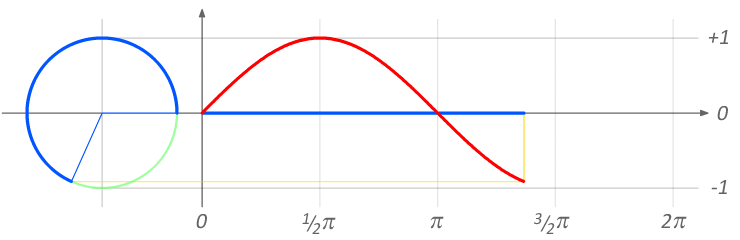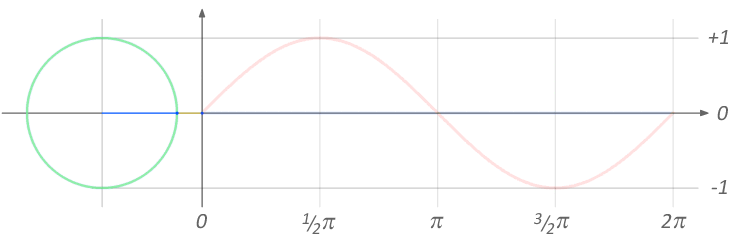
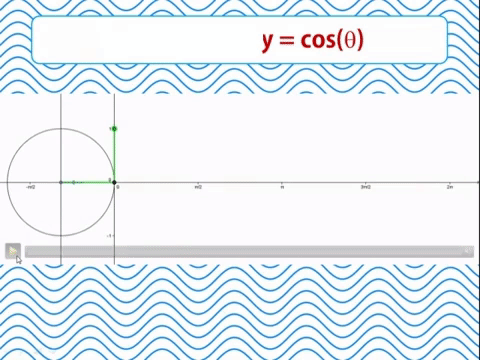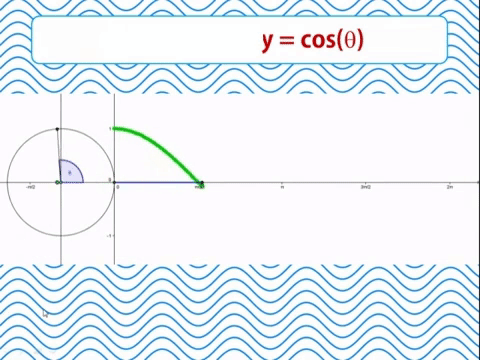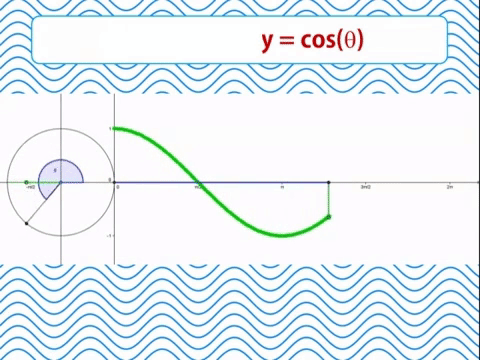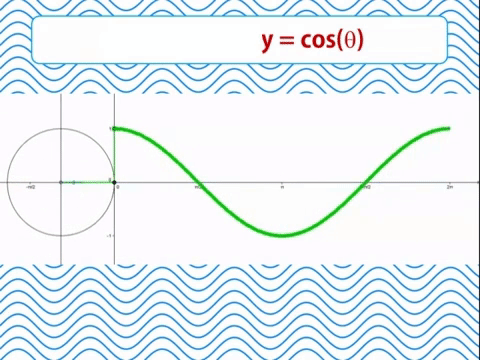
Función coseno

En un ángulo interno en el círculo trigonométrico cuyos segmentos son igual al radio 1, el coseno será la proyección del segmento móvil sobre el eje de las abscisas X. Imaginemos una linterna iluminando este segmento móvil dentro del círculo. La sombra que proyecta el segmento sobre el eje X será el valor del coseno.
Cuando se grafica el coseno a medida que el segmento se abre, el coseno se reduce hasta ser igual a 0 cuando el ángulo es igual a 90º o 1/2π. Desde los 90º a los 270º el coseno toma valores negativos. Por encima de los 270º el coseno vuelve a tomar valores positivos hasta llegar a 1 en los 360º. Los valores del coseno se hallan entre 1 y -1.
Función tangente

.
Comentarios
Publicar un comentario